| Model Theory | examines relationships between formal languages and mathematical structures. In PL, it provides the foundation for type systems and formal semantics, offering frameworks to understand how programs denote mathematical objects and how logical specifications correspond to program behavior. While classical model theory often deals with infinite structures, finite model theory is particularly relevant to program verification and synthesis, where it enables techniques like model checking and automated reasoning over bounded domains, supporting both correctness verification and synthesis from specs. |
|---|---|
| Proof Theory | studies formal proofs as mathematical objects. Through the Curry-Howard isomorphism, it connects directly to type systems in FP, where programs are proofs and types are propositions. Its concepts underpin type checkers, theorem provers, and formal verification tools. |
| Set Theory | forms the mathematical basis for denotational semantics, where programs are interpreted as operations on well-defined mathematical objects. Domain theory, built on set-theoretic foundations, provides models for recursive definitions and is essential for understanding language semantics. |
| Recursion Theory | aka the famous Computability Theory, establishes the fundamental limits of computation. Its results on undecidability (like Rice's theorem) directly impact program analysis, while fixed-point theorems provide the foundation for understanding recursive programs and iterative algorithms. |
Math Motivations
-
LogicThere are four branches of modern mathematical logic, all of which provide crucial foundations for PL.
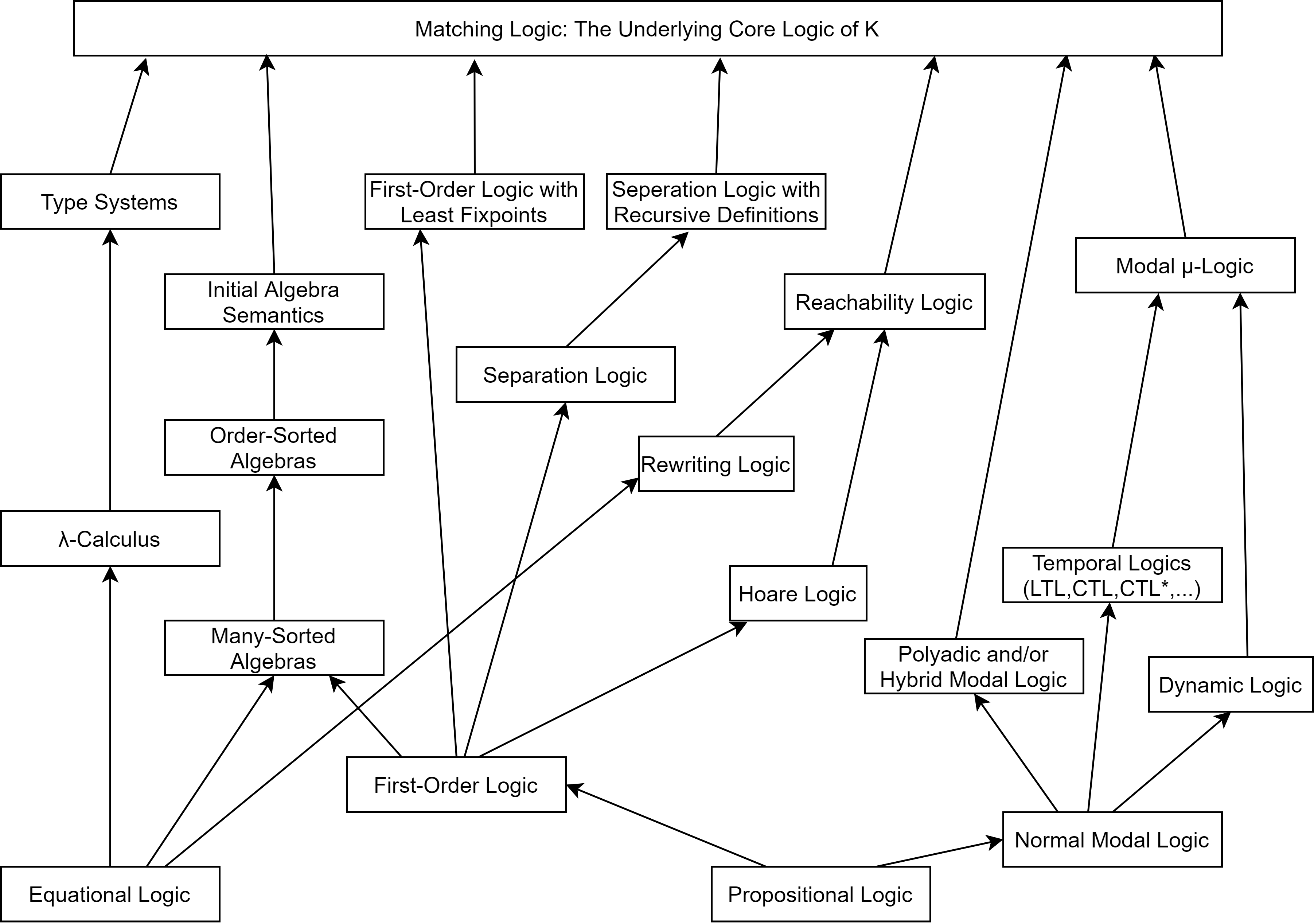
Figure: A possible hierarchy of logics from matching logic framework. -
AlgebraAlgebraic structures provide powerful frameworks for reasoning about computation (unexpectedly) and program behavior.
Order Theory studies mathematical structures with ordering relations. In static analysis, it provides the framework for data flow analysis and abstract interpretation. Lattices and fixed points are essential for program optimization and verification techniques. Universal Algebra studies common properties of algebraic structures. In PL, it directly informs the design of algebraic data types and algebraic effects. Initial algebras and coalgebras provide the mathematical foundations for defining inductive and coinductive data types in functional languages. -
Category Theory"Nobody understands category theory" - David Spivak
Basics Category Theory provides an abstract framework for describing mathematical structures and their relationships. In FP, concepts like functors and monads offer powerful abstractions for managing effects and composing programs. Cartesian Closed Categories (CCCs) specifically provide a mathematical model for $\lambda$-calculus and typed functional languages, elegantly capturing the semantics of products (tuples) and exponentials (functions). This unified framework helps explain higher-order functions, type systems, and forms the theoretical foundation for many modern language features. HoTT unifies type theory with homotopy theory, viewing types as spaces and functions as continuous mappings. In PL, it provides a foundation for dependent type systems with identity types that capture equality in a more fundamental way. HoTT's univalence principle offers powerful abstraction mechanisms for program verification and formalization of mathematics, influencing the design of proof assistants and dependently-typed languages.